Credit Valuation Adjustment
Keywords: CVA, Incremental CVA, DVA, Incremental DVA, Bilateral CVA
Credit valuation adjustment (CVA) is the difference between the risk-free portfolio value and the true portfolio value that takes into account the possibility of a counterparty’s default. In other words, CVA is the market value of counterparty credit risk.
Unilateral CVA is given by the risk-neutral expectation of the discounted loss. The risk-neutral expectation can be written as
where L* is the discounted loss, T is the maturity of the longest transaction in the portfolio, Bt is the future value of one unit of the base currency invested today at the prevailing interest rate for maturity t, R is the fraction of the portfolio value that can be recovered in case of a default, τ is the time of default, E(t) is the exposure at time t, PD(s, t), is the risk neutral probability of counterparty default between times s and t. These probabilities can be obtained from the term structure of credit default swap (CDS) spreads.
More generally CVA can refer to a few different concepts:
- The mathematical concept as defined above;
- A part of the regulatory Capital and RWA (Risk weighted asset) calculation introduced under Basel 3;
- The CVA desk of an investment bank, whose purpose is to:
- hedge for possible losses due to counterparty default;
- hedge to reduce the amount of capital required under the CVA calculation of Basel 3;
- The “CVA charge”. The hedging of the CVA desk has a cost associated to it, i. e. the bank has to buy the hedging instrument. This cost is then allocated to each business line of an investment bank (usually as a contra revenue). This allocated cost is called the “CVA Charge”.
Exposure, independent of counterparty default
Assuming independence between exposure and counterparty’s credit quality greatly simplifies the analysis. Under this assumption this simplifies to
Where EE* is the risk-neutral discounted expected exposure (EE)
Debt Valuation Adjustment – Debt Valuation Adjustment. (DVA) is an accounting valuation technique related to how a company handles changes in its issued fixed income securities. According to FASB 159 (adopted in 2007), firms can recognize market value declines in some debt instruments as earnings (income).
Use of this valuation method is optional for reporting companies, and can be adopted on a security by security basis (vs. applying to all outstanding bonds, for example). An interesting aspect of the rule is that once reporting companies adopt this rule for certain securities, switching to a different valuation technique is prohibited.
This valuation technique was used by financial firms in 2008 as a way to minimize accounting losses: as the market value of issued debt declined, companies would recognize the decline as income.
Considering that declines in market value of debt could signal future problems for a company (namely a higher cost of debt and interest burden), investors should evaluate the full implications of DVA on the long term condition of a firm and the quality of earnings affected by DVA. For example, if a \\$100 par bond has a DVA to \\$50, the company will still need to pay the bondholder $100 at maturity (either from cash or financed with more debt, which would likely be at a higher interest rate).
In Kamakura Risk Manager (KRM) CVA/DVA, and incremental CVA approach involves simulation modelling of market risk factors and risk factor simulations, and then revaluing each derivative instrument with user-specified time steps and number of scenarios using the counterparty’s and the organisation’s own market implied credit spread term structure. The resulting matrix of simulations by scenario and time steps is then aggregated to generate expected collateralized exposure profile for each netting counterparty.
Figure 1 – User-defined risk factors
Figure 2 – User-defined risk factor distributions
Figure 3 – User-defined time steps
KRM generates the following CVA related measures of each netting set:
- CVA
- Incremental CVA for each transaction in the netting set
- DVA
- Incremental DVA for each transaction in the netting set
- BCVA
Bilateral CVA (BCVA) is taking into account first to default.
In KRM, the user can choose whether to turn on first-to-default (FTD) feature in Bilateral CVA (BCVA) calculation.
When FTD option is turned off, BCVA is the netted result of Unilateral CVA and DVA.
When FTD option is turned on, KRM uses the counterparty’s and the bank’s own instantaneous hazard rate and default correlations to simulate default events within each CVA time step, where
Time-to-default (TTD) = – ln (random number) / instantaneous hazard rate
Therefore in a simulation scenario,
⦁ If TTD (bank) is after TTD (counterparty), i.e. counterparty defaults first, CVA will be reduced.
⦁ If TTD (bank) is before TTD (counterparty), i.e. bank defaults first, DVA will be reduced.
KRM computes BCVA with FTD option accordingly.
Figure 10 – Counterparty and the Banks’s default correlation
Figure 11 – Sample Report for CVA, DVA and BCVA with and without FTD under different default correlation levels
PFE (Potential Future Exposure), Average PFE, Effective PFE, indicating any ability to customise observation dates
EPE (Expected Positive Exposure), Average EPE, Effective EPE, indicating any ability to customise observation dates
ENE (Expected Negative Exposure), Average ENE, Effective ENE, indicating any ability to customise observation dates
EE (Expected Exposure), Average EE, Effective EE, indicating any ability to customise observation dates
Potential Future Exposure Amount
Potential future exposure measures are usually employed in the context of financial instruments, where they refer to the future replacement cost of a financial contract in the event it is has to be terminated by a counterparty default, or for any other reason. The future replacement cost would be the value of the financial instrument from the viewpoint of the portfolio holder, assuming it is positive. (If it is negative, there is no replacement cost.) Since the future value of a financial instrument is uncertain and varies as a function of uncertain future interest rates, foreign exchange rates, equity prices and other risk drivers, the measures of potential future exposure must be defined in terms of a probability distribution of the value of the instrument at a future point in time.
Two of the measures relate to statistics of this probability distribution: expected future exposure and maximum future exposure. Expected future exposure is the mean of the probability distribution of future value as of a given future time (or for a future time band). Maximum future exposure is the value corresponding to a specified percentile (e.g. 95%) as of a given future time (or for a future time band) of the future value distribution, which would only be exceeded infrequently – it represents an extreme measure of future value that would be more conservative than the expected future exposure.
The other two potential future exposure measures relate to the maximum future exposure measure: peak future exposure and average maximum future exposure. These measures are designed to reflect future exposure over the entire future time-period prior to the final exercise date of a financial instrument rather than just a single future point in time. Peak future exposure represents the maximum value of the maximum future exposure measure across all future points in time, so it indicates the largest value of the extreme measure of value over the future time-period. On the other hand, average maximum future exposure represents the average value of the maximum future exposure measure across all future points in time, so it effectively smoothens the extreme measure over the future time period. These latter two measures are typically approximated by determining maximum future exposure for a sequence of points in time in the future time-period.
Since all of these measures are defined in terms of the probability distribution of future value of an individual financial instrument or a portfolio of financial instruments, the primary function is to construct an empirical distribution of potential future values for one or more future points in time. This is typically accomplished by performing a Monte Carlo simulation of the underlying interest rates, foreign exchange rates, equity prices and other risk drivers over the time interval up to each future point in time and then using the resulting yield curve and risk driver scenarios to calculate the values of the financial instrument or portfolio at the future time.
This is, of course, the same process that is followed in Kamakura Risk Manager (KRM) to obtain the empirical probability distribution of values that is used to estimate Value at Risk using the Monte Carlo approach, so KRM incorporates the underlying capabilities needed to calculate all the potential future exposure measures. Once these capabilities have been used to calculate the future value distribution for a given future date, the expected future exposure and maximum future exposure measures can be directly calculated from the empirical distribution. By using these capabilities repetitively for a sequence of future dates, the maximum future exposure measures for each date in the sequence can be used to directly calculate the peak future exposure and average maximum future exposure measures.
It should be pointed out that future financial instrument values are usually calculated using default-free or swap yield curves for valuation, so these values are not credit-adjusted values and do not require counterparty default or obligation recovery models for their calculation. This means that it is not strictly necessary to have KRM-cr to estimate these values, although credit models and KRM-cr would be needed to calculate expected credit losses and economic capital based on the potential future exposure measures.
The following graph represents the potential future exposure on an interest rate swap over the life of the swap. This effectively represents the dynamic market (or model) values of the swap up to maturity.
PFE measures can be calculated for an individual financial instrument or for any collection of financial instruments. Since these measures are typically used to assess the potential credit exposure to a credit-risky counterparty, the collection of all financial instruments where the counterparty is a specific credit-risky entity (sometimes called a counterparty sub-portfolio) is of primary interest in calculating PFEs. This counterparty sub-portfolio can be selected using a counterparty identifier associated with each financial instrument position held in a portfolio.
KRM provides capabilities to generate the empirical probability distribution of future financial instrument values that is required to estimate the aforementioned PFE measures. These capabilities include:
- Modelling yield curve term structures, which is provided by the KRM-yc functionality;
- Modelling risk drivers (such as spot foreign exchange rates, equity indices, etc.), which is provided by the KRM-var functionality;
- Simulating the evolution of yield curves and risk drivers from the current date to the future date for PFE calculations using Monte Carlo simulation techniques, which is provided by the KRM-var functionality;
- Identifying individual financial instrument positions with specific counterparty entities, which is provided by the basic KRM database functionality; and
- Valuing the financial instruments using the evolved yield curves and risk drivers on the future date for PFE calculations (future mark-to-model), which is provided by a combination of the KRM-mv and KRM-var functionality.
The Monte Carlo simulation process performed using these capabilities can produce both positive and negative values for various financial instruments. For example, an interest rate swap can have either a positive or a negative value depending upon whether the holder receives fixed or floating and whether swap rates on the future date for PFE calculations are higher or lower than the swap contractual rate. Since only positive values reflect a credit exposure, all negative values produced by the Monte Carlo simulation must be eliminated to produce the distribution of replacement values. Additionally, each positive replacement value must be associated with the counterparty to the financial instrument, so that the PFE measures can be calculated for a specific counterparty. The result is an empirical or sample distribution of replacement values for every counterparty, and these results can be used to calculate the PFE measures for that counterparty. The expected future exposure PFE measure is calculated as the mean of the empirical distribution, and the maximum future exposure PFE measure is calculated as the specified percentile (e.g. 95%) of the empirical distribution.
KRM currently has the capabilities to determine the future value of a wide range of interest rate, foreign exchange, and equity financial instruments.
Marginal PFE re-calculations can also be performed efficiently using the KRM capabilities discussed here. In particular, the same yield curve and risk driver scenarios produced by the KRM simulation can be used to estimate the future replacement value of additions to an existing financial instrument portfolio. This does not involve any recalculation of the future replacement value of positions in the existing financial instrument portfolio. The resulting future replacement values for the portfolio additions can be combined with the results produced for the existing portfolio, and the future replacement values for the combined portfolio can then be used to estimate the PFE measures. This approach allows the marginal PFE calculations to be performed very efficiently.
The KRM solution can model and calculate potential future exposure (PFE) metrics for counterparty risk exposures, including derivative instruments, reinsurance, and other bilateral contracts. These metrics are required because the exposure amounts of the derivative instruments and other bilateral contracts vary over time and the exposure amount at a future default time is often much larger than the current replacement cost. KRM currently provides two approaches to modelling and measuring PFE: a current exposure method (CEM, consistent with the Basel II/III Current Exposure Method) and an internal model method (IMM, consistent with the Basel II/III Internal Model Method) for calculating PFE metrics.
Current Exposure Method
Under the CEM, the exposure amount at default EAD(D,t) of a derivative instrument counterparty credit exposure D at time t is the sum of the current replacement cost of the exposure CRC(D,t) and a PFE ‘add-on’ amount AOA(D,t) at time t, i.e.
EAD(D,t) = CRC(D,t) + AOA(D,t)
The current replacement cost CRC(D,t) of a derivative instrument counterparty credit exposure at time t is its credit-adjusted economic value V(D,t) at time t when EAD(D,t) is calculated, if positive, and zero otherwise, i.e.
CRC(D,t) = max{0,V(D,t)}
The KRM Analytical Engine calculates the credit-adjusted economic value V(D,t) of a derivative instrument using the Monte Carlo pricing methods for defaultable bilateral derivative contracts.
The PFE ‘add-on’ amount AOA(D,t) at time t is calculated as the product of the notional amount of the exposure NA(D,t) at time t and an add-on factor AOF(D,t) at time t, i.e.
AOA(D,t) = NA(D,t) * AOF(D,t)
The add-on factor AOF(D,t) is determined by the residual maturity of the exposure t at time and the type of asset (interest rate, FX, etc.) underlying the exposure, based on specified add-on factor percentages for various maturity range and underlying asset categories. The KRM solution maps the maturity and asset category of each derivative instrument to a maturity range and underlying asset category, assigns the corresponding AOF(D,t) to the instrument, and uses it to calculate the AOA(D,t) for the instrument at time t.
The KRM solution also can calculate net exposure amounts under the CEM for counterparty risk exposures covered by collateral agreements. KRM models collateral agreements as credit derivative instruments. The KRM Analytical Engine can calculate the current economic value of the collateral pool associated with a collateral agreement covering a counterparty risk exposure, and the adjusted exposure amount at default AEAD(D,t) of the exposure D at time t is calculated as the difference between the unadjusted exposure amount at default EAD(D,t) of the instrument and the current economic value of the collateral pool V(C,t), if positive, and zero otherwise, i.e.
AEAD(D,t) = max ({(EAD(D,t) – V(C,t)),0}
Internal Model Method
The IMM provides a sophisticated and more accurate approach to estimate the exposure amount at default EAD(D,t) of a derivative instrument counterparty credit exposure D at a given time t. Under the IMM, the exposure amount at default EAD(D,t) of a counterparty credit exposure D is calculated using sample distributions of exposure amounts 
at a sequence of future tenor points 
where t is a tenor point that equals or exceeds the remaining time to expiration of the counterparty credit exposure 
denotes a particular sample path of the exposure risk factor vector 
applicable to the exposure 
is the value of the exposure risk factor vector at the time 
The tenor points correspond to future points in time 
relative to the time t when EAD(D,t) is calculated. The PFE calculations under the IMM are relatively complex, as is shown in the following discussion.
The exposure risk factor vector 
is the set of market and macroeconomic risk factors, such as interest rates, foreign exchange rates, inflation rates, etc., affecting the 
amounts of the counterparty credit exposure that provide the input values required to calculate the credit-adjusted value of the counterparty credit exposure at a given point in time. For example, if the counterparty credit exposure is a defaultable OTC European-style call option on an equity security, its credit-adjusted economic value depends upon the price of the underlying equity security on the valuation date. When the valuation date is a future date, this price is unknown and must be modelled as a stochastic process describing changes in the equity price over time. This process is often modelled using an asset return model that describes a linear relationship between returns on the equity security and returns on an equity market index and/or other risk factors with the equity security’s value sensitivity to each risk factor being described by its beta. The equity market index is modelled as a component of the exposure risk factor vector 
to provide the input to the asset return model and to calculate the future equity security price.
To support credit-adjusted valuation of the derivative instrument, the exposure risk factor vector 
must also include component risk factors affecting the default behaviour of the counterparties to the instrument and affecting the value recovery rates for the instrument for each counterparty. The values of these risk factors on the valuation date for the counterparty risk exposure provide the initial default intensity risk factor values for the default intensity models of the counterparties and the initial value recovery risk factor values for the value recovery process models for the exposure for each counterparty. Thus collectively the exposure risk factor vector 
consists of one or more asset value risk factors, one or more default behaviour risk factors for each counterparty, and one or more value recovery risk factors for each counterparty.
KRM simulates sample paths of the exposure risk factor vector 
to provide the inputs for credit-adjusted valuation of each derivative instrument. The KRM solution uses historical or Monte Carlo simulation methods to simulate the required sample paths.
KRM uses the simulated sample paths of the exposure risk factor vector 
to calculate the future exposure amounts 
of the derivative instrumentD as the future replacement cost of the instrument, which is the credit-adjusted economic value 
of the instrument at time 
on sample path j if positive, and zero otherwise. Thus the future exposure amounts 
are
The KRM Analytical Engine calculates the credit-adjusted economic value 
of a counterparty credit exposure at time 
using the simulated exposure risk factor vector 
by applying the Monte Carlo pricing methods for defaultable bilateral derivative contracts.
The PFE simulation performed by the KRM Analytical Engine produces a sample distribution of potential exposure amounts 
for the derivative instrument D across the sample paths 
of the exposure risk factor vector 
at each future tenor point 
. These sample distributions can be used to calculate various PFE metrics for the derivative instrument D over the simulation horizon T.
The KRM solution also can calculate net exposure amounts under the IMM for counterparty risk exposures covered by collateral agreements. KRM models collateral agreements as credit derivative instruments. The KRM Analytical Engine can calculate the adjusted economic value 
of the collateral pool associated with a collateral agreement 
covering a counterparty risk exposure on each sample path 
of the exposure risk factor vector 
at each future tenor point 
. The adjusted value of the collateral pool 
is the sum of the values 
of the n collateral items in the pool at time 
i.e.
The value 
of a collateral item 
is the product of the adjusted economic value 
of the collateral asset 
associated with the collateral item 
multiplied by the portion 
of the collateral asset value allocated to the collateral item, i.e.
The adjusted economic value 
of a collateral asset 
is the economic value 
of the collateral asset 
less adjustments for collateral asset value volatility 
foreign exchange volatility 
and maturity mismatch with the tenor of the collateral agreement that the collateral asset underlies 
i.e.
The collateral asset volatility adjustment amount 
is equal to the product of the credit-adjusted value of the collateral asset 
on sample path multiplied by the asset volatility haircut percentage for the asset 
on sample path between the currency denomination of the collateral asset 
and the currency denomination of the collateral agreement 
(which is 1 if the collateral agreement and the collateral asset are denominated in the same currency), i.e.
When the collateral asset 
is denominated in the same currency as the collateral agreement 
the foreign currency collateral asset adjustment amount 
is equal to zero, i.e.
When the collateral asset is denominated in a different currency from the collateral agreement 
the product of the credit-adjusted value of the collateral asset 
multiplied by the foreign exchange volatility haircut percentage for the asset
between the currency denomination of the collateral asset 
and the currency denomination of the collateral agreement 
(which is 1 if the collateral agreement and the collateral asset are denominated in the same currency), i.e.
The effective maturity collateral asset adjustment amount 
is equal to the product of the credit-adjusted value of the collateral asset 
, a haircut factor 
, and the spot FX rate 
between the currency denomination of the collateral asset 
and the currency denomination of the collateral agreement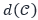 
, i.e.
where the haircut factor 
reduces the collateral asset value by the asset volatility and foreign exchange haircuts, i.e.
and where the maturity factor 
is calculated using the following formula that incorporates the remaining tenor to maturity of the credit exposure 
and the remaining tenor to maturity of the collateral agreement 
The KRM Analytical Engine can calculate the adjusted value of the collateral pool 
for each of the tenor points 
, when performing the counterparty credit exposure simulations discussed earlier in this section. Note that this can involve several collateral asset valuations at each tenor point on each sample path of the exposure risk factor vector for the collateral agreement. Since an exposure risk factor vector value is required for valuation of each collateral asset and initial values of the exposure risk factor vector are required for each component risk factor in the valuation risk factor vector, the exposure risk factor vector path must include values for all of the component risk factors in the valuation risk factor vectors of all of the collateral assets underlying the collateral agreement. In general, this requires additional component risk factors in the exposure risk factor vector for the same counterparty credit exposure if it is uncollateralized, and an expanded exposure risk factor vector incorporating these additional component risk factors is used to perform the exposure simulation.
The KRM Analytical Engine also calculates the exposure amounts at default 
of a collateralized derivative instrument credit exposure 
covered by a collateral agreement 
on each expanded exposure risk factor vector sample path 
. The exposure amounts at default 
of a collateralized counterparty credit exposure at each future time 
are calculated as the excess, if any, of the volatility-adjusted exposure amount 
of the exposure over the adjusted economic value of the collateral pool 
, i.e.
where the volatility-adjusted exposure amount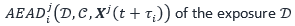 
is the product of the uncollateralized credit exposure amount 
calculated as previously described and a factor based on the exposure value volatility 
that increases the exposure amount, i.e.
The KRM Analytical Engine retains the results of these calculations in the KRM Database, and it uses the exposure amounts at default 
of a collateralized counterparty credit exposure in place of the exposure amounts at default 
of the same exposure if uncollateralized to perform the PFE calculations for the exposure outlined earlier.
KRM generates comprehensive Counterparty Risk Measures (CCR) measures using full Monte Carlo simulation, with user defined time steps and observation dates.
KRM can store all the netting set information, including exposure and collateral items with allocation percentages, etc. KRM generates the following CCR measures of each netting set:
- PFE
- EE and Effective EE
- EPE and Effective EPE
- ENE and Effective ENE
- EAD of CEM (MtM + add-on) and IMM (α*Effective EPE) methods
Wrong way risk – general
Wrong way risk – specific
KRM incorporates wrong way risk (WWR) in Counterparty Credit Risk (CCR) measures and CVA by adding correlation in market-credit risk factor set (for general WWR) and default correlation between counterparty and the reference entity (for a common case of specific WWR)
Figure 13 – Market- Credit risk factor sets
Figure 14 – Risk factor correlations
Figure 15 – Generic and Specific WWR at different correlation levels
FVA, indicating any ability to customise observation dates
The subject-matter expertise within Kamakura Corporation believes that rather than use a funding spread on market values, it would be a better option to generate FVA based on cashflow changes due to additional funding costs. However, both approaches can be clearly modelled within KRM.
Option 1
Generate the first scenario based on no funding costs for the user-defined time steps, and thereafter, generate the same cashflows after incorporating the credit spreads. The difference would be the FVA of the portfolio.
Option 2
As outlined above, use the bank’s funding spread to compute the market value on a dynamic basis for the portfolio and for each time step therefore, the FVA can be computed.
CVA according to the Basel III standardized method
KRM supports EAD using CEM (MtM + Add-on) and IMM (α*Effective EPE) methods, and user can select either CEM or IMM EAD in the standardized CVA capital charge formula, and between standardized and advanced approach.
