Basel Credit Risk
EXECUTIVE SUMMARY
An important element of Basel III is the definition of minimum capital adequacy requirements for counterparty credit exposures (derivative instruments, long settlement transactions, securities financing transactions, and counterparty master agreements where the counterparty to the transaction is a credit-risky entity) held by banks.
Basel III defines two forms of capital adequacy requirements for counterparty credit exposures. The first form specifies the minimum capital required to cover potential future losses from counterparty defaults in terms of the probability of
counterparty default (PD), the loss rate given default (LGD) on a defaulted exposure, the exposure at default (EAD) of the exposure, and the effective maturity (M) of the exposure. The second form specifies the minimum capital required to cover potential future losses from future changes in the credit quality of the counterparty that result in changes in the credit spreads for the counterparty’s credit exposures.
Pillar 1 of Basel III requires that banks satisfy these minimum capital requirements at all times. In addition, Pillar 2 of Basel III requires that banks establish plans for capital resources sufficient to satisfy the capital requirements in future periods, which requires forecasts of future capital requirements.
Capital adequacy requirements under Basel III are calculated using a potential future exposure (PFE) approach, where future credit exposure amounts for a counterparty credit exposure are estimated and used to determine the exposure at default (EAD) amount for the counterparty credit exposure. Basel III provides three alternative methods for estimating future
exposure amounts the Current Exposure Method, the Standardized Method, and the Internal Model Method. Moreover, the KRM solution supports the collateral management process enabling the optimal allocation of collaterals to exposures. Our consultants perform this task under the objectives of the optimisation procedure specified by the bank. (minimising capital charge, reputation risks, level of complexity desired etc).
The fact that there are numerous successful implementation projects in the entire region is a great plus for Kamakura, and is testimony to the credentials of Kamakura’s subject matter experts. Kamakura is well-positioned to meet the burgeoning
regulatory demands imposed on financial institutions in the region and has the wherewithal to keep pace with regulation. Among others, Kamakura has undertaken a number of litigation support projects and is prepared to provide expert testimony supported by methodical analysis employing the KRM system.
KEY BENEFITS AND FEATURES
1. Basel III Expected Exposure (EE) Forecast for Future Periods
The exposure risk factor (ERF) vector and the yield curves as well as their associated stochastic process models are required to simulate the specific sources of risk affecting the future economic values of the derivative instruments, and both the derivative instrument, and collateral pool valuation models are required to calculate future economic values of the derivative instruments and any collateral agreement covering it based upon the projected future values of the ERF vector and the yield curves.
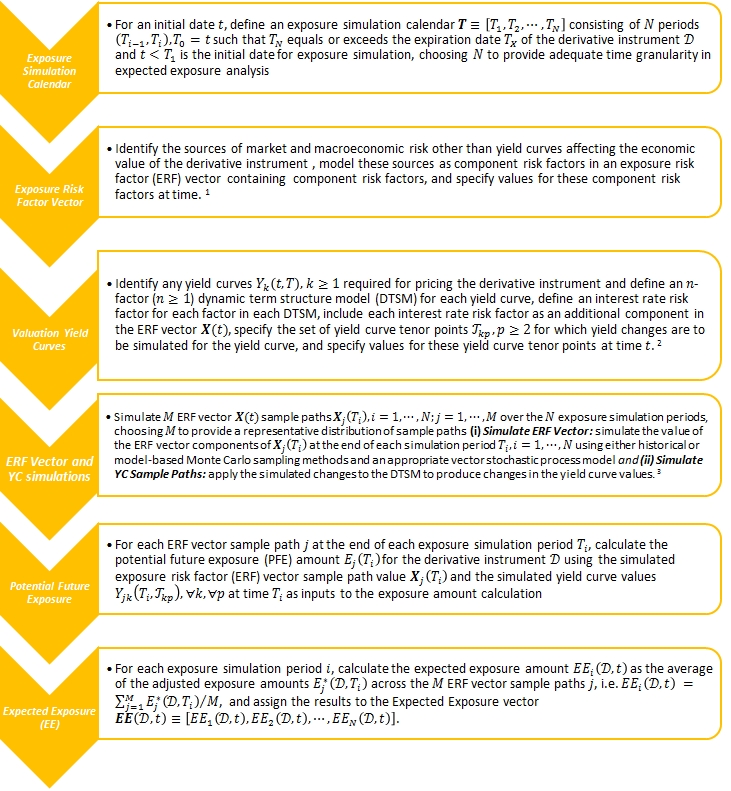
Simulation Calendar
RM will aggregate the information into user-defined time buckets referred to as Accounting Periods. Each Accounting Period ID will be linked to a specific range of forecast dates (i.e., beginning date and ending date).
Exposure Risk Factor Vector
Modelling risk drivers (such as spot foreign exchange rates, equity indices, etc.), which is provided by the KRM-var
functionality.
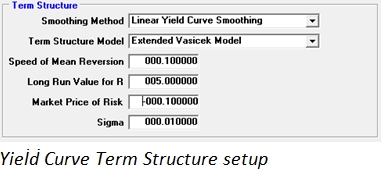
Yield Curve Term Structure
Term structure models for the modeling of the evolution of the yield curve are absolutely critical for the valuation of most derivative securities. Neither implied forward rates nor selected, deterministic, forecasts of future rates provide sufficiently accurate, unbiased predictions. The KRM solution supports Advanced Heath Jarrow & Morton Interest Rate Modeling which is the most general model consistent with a no arbitrage multi-factor evolution of the yield curve (every model used in industry is a special case of the general structure). Also the KRM solution allows an arbitrary number of risk factors (KRM can handle up to 999,999!!!).
Advanced stress testing
Provides a deeper understanding of the portfolio with detailed scenario by simulating the evolution of yield curves and risk drivers from the current date to the future date for PFE calculations using Monte Carlo simulation techniques, which is provided by the KRM-var functionality
2. Basel III Exposure at Default (EAD) and Effective Maturity (M)
The Exposure at Default and Effective Maturity metrics are point-in-time counterparty exposure metrics required to support the credit risk capital requirement calculations discussed in Section III. Credit Risk – The Internal Ratings-Based Approach of the Basel II guidelines. The KRM solution supports the Exposure at Default and Effective Maturity metrics calculations according to the procedures specified in paragraphs 27 to 39 of Annex 4 of the Basel II guidelines.

3. Basel III Default Risk Capital Requirement Forecast
The Exposure at Default and Effective Maturity metrics are point-in-time counterparty exposure metrics required to support the credit risk capital requirement calculations discussed in Section III. Credit Risk – The Internal Ratings-Based Approach of the Basel II guidelines. The KRM solution supports the Exposure at Default and Effective Maturity metrics calculations according to the procedures specified in paragraphs 27 to 39 of Annex 4 of the Basel II guidelines.
- Standardized Approach
- Foundation IRB
- Advanced IRB
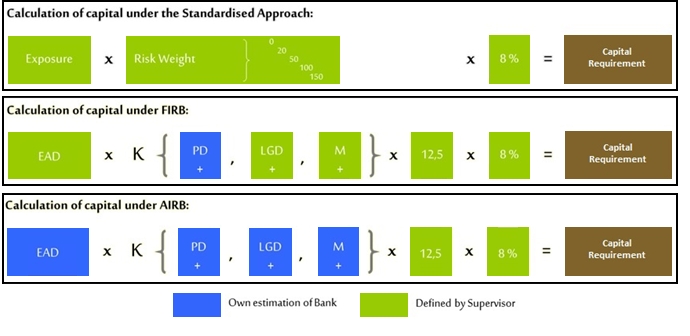
The credit risk component values required to calculate risk-weighted asset and capital requirement amounts under the Basel II/III Internal Ratings Based (IRB) Advanced Approach for default risk capital adequacy are the Probability of Default (PD), Loss Rate Given Default (LGD), Exposure at Default (EAD), and the Effective Maturity (M) for the derivative instrument.
Regulatory Compliance
The KRM Solution offers organizations the tools required for calculating Regulatory Capital requirements. Moreover, it allows users to simultaneously calculate Regulatory Capital under any of the abovementioned approaches.
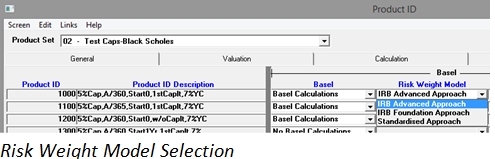
Local Regulatory Compliance
The KRM Solution can be easily configured to meet the parameterization of local regulations.
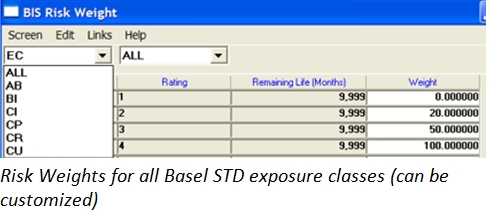
Reporting
- A wide range of pre-defined reports is available. It enables users to create user-defined outputs which
can be used to create ad-hoc reports. - The Dashboard Designer is an intuitive tool used for building and modifying reports.
- Different objects types such as charts, tables and filters are being combined to a dashboard.
4. XVA – Credit Valuation Adjustments/Debt Valuation Adjustments/Funding Valuation
Adjustments
4.1 Basel III Credit Valuation Adjustment (CVA)
The Credit Valuation Adjustment value of the derivative instrument is a point-in-time counterparty valuation metric[1].
Evaluation of this formula is required to calculate the Advanced CVA risk capital charge for derivative instruments [2]. The regulatory formula for the CVA value presented in paragraph 98 is of the following form:

4.2 Basel III CVA according to the Basel III standardized method
The formula proposed by the Basel Committee for the standardized approach is a Value At-Risk model with 99% confidence level and 1 year time horizon.
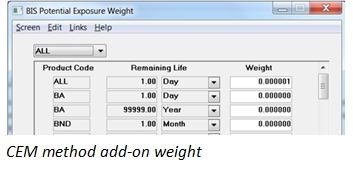
KRM supports EAD using CEM (MtM + Add-on) and IMM (α*Effective EPE) methods, and user can select either CEM or IMM EAD in the standardized CVA capital charge formula, and between standardized and advanced approach.
4.3 Debt Valuation Adjustment, Bilateral CVA and Funding Valuation Adjustment Debt Valuation Adjustment
It is an accounting valuation technique related to how a company handles changes in its issued fixed income securities. According to FASB 159 (adopted in 2007), firms can recognize market value declines in some debt instruments as earnings (income).
Use of this valuation method is optional for reporting companies, and can be adopted on a security by security basis (vs. applying to all outstanding bonds, for example). An interesting aspect of the rule is that once reporting companies adopt this rule for certain securities, switching to a different valuation technique is prohibited.
Bilateral CVA
In KRM, the user can choose whether to turn on first-to-default (FTD) feature in Bilateral CVA (BCVA) calculation.
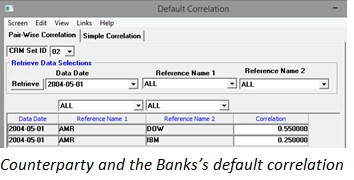
When FTD option is turned off, BCVA is the netted result of Unilateral CVA and DVA. When FTD option is turned on, KRM uses the counterparty’s and the bank’s own instantaneous hazard rate and default correlations (as shown in the Figure) to simulate default events within each CVA time step.
Therefore in a simulation scenario,
- If TTD (bank) is after TTD (counterparty), i.e. counterparty defaults first, CVA will be reduced.
- If TTD (bank) is before TTD (counterparty), i.e. bank defaults first, DVA will be reduced.
Funding Valuation Adjustments
While there is no common market standard for FVA calculation, one approach of FVA calculation is that FVA = the bank’s funding spread * EE of the portfolio, which can be easily computed in KRM. The subject-matter expertise within Kamakura Corporation believes that rather than use a funding spread on market values, it would be a better option to generate FVA based on cashflow changes due to additional funding costs. However, both approaches can be clearly modelled within KRM.
Option 1
Generate the first scenario based on no funding costs for the user-defined time steps, and thereafter, generate the same cashflows after incorporating the credit spreads. The difference would be the FVA of the portfolio.
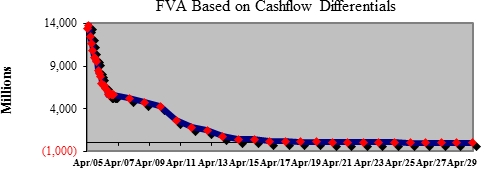
Option 2
As outlined above, use the bank’s funding spread to compute the market value on a dynamic basis for the portfolio and for each time step therefore, the FVA can be computed.
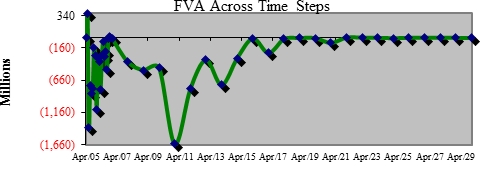
Reporting
KRM generates the following CVA related measures of each netting set:
- Credit Valuation Adjustments (CVA)
- Incremental CVA for each transaction in the netting set
- Debt Valuation Adjustments (DBA)
- Incremental DVA for each transaction in the netting set
- Bilateral CVA (BCVA)
- Incremental BCVA for each transaction in the netting set
- Funding Valuation Adjustments
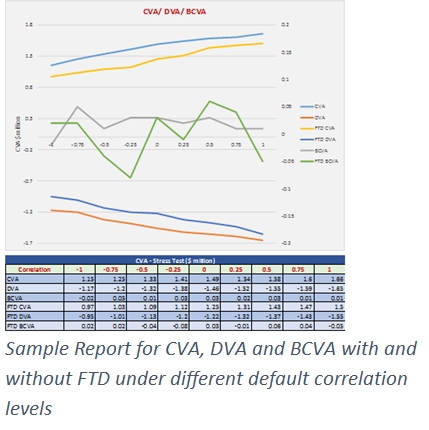
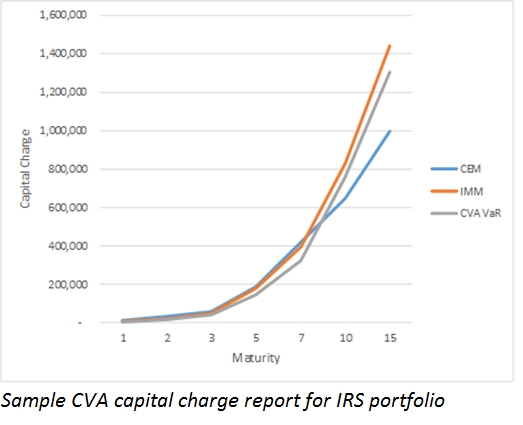
5. Basel III CVA Capital Charge Forecast
The CVA Capital Charge CVACC(T_i^’ ) for the time period with end date T_i^’ in T^’ is calculated as the Credit Valuation Adjustment Value at Risk for the sub-portfolio at the 99th percentile one-tailed confidence level over a 10 trading day holding period. The forecasts of the Basel III CVA Capital Charge are time period counterparty risk metrics that provide the basis for estimating a bank’s capital requirements for counterparty credit risk produced by changes in credit spreads in future periods.