ABSTRACT
This paper analyzes the number and the nature of factors driving the movements in the Japanese Government Bond yield curve from September 24, 1974 through December 28, 2018. The process of model implementation reveals a number of important insights for interest rate modeling generally. First, model validation of observed yields is important because those yields are the product of a third-party curve fitting process that may produce spurious indications of interest rate volatility. Second, quantitative measures of smoothness and international comparisons of smoothness provide a basis for measuring data quality. Third, we outline a process for incorporating insights from the Japanese experience with negative interest rates into term structure models with stochastic volatility in other countries. Finally, we illustrate the process for comparing stochastic volatility and affine models of the term structure. We conclude that stochastic volatility models have a superior fit to the history of yield movements in the Japanese Government Bond market.
Government yield curves are a critical input to the risk management calculations of central banks, bank regulators, major banks, insurance firms, fund managers, pension funds, and endowments around the world. With the internationalization of fixed income investing, it is important to understand the dynamics of movements in yield curves world-wide, in addition to the major bond markets like those in Frankfurt, London, New York and Tokyo. In this paper, we fit a multi-factor Heath, Jarrow and Morton model to daily data from the Japanese Government Bond market over the period from September 24, 1974 to December 28, 2018. The modeling process reveals a number of important implications for term structure modeling in other government bond markets.
Section I discusses the origin and characteristics of the daily data base of Japanese Government Bond yields provided by the Ministry of Finance in Japan. Model validation on the raw data in the data base reveals a higher degree of variation in forward rates, even when fit on a “maximum smoothness” basis, than is typical of international markets. We quantify the differences in smoothness by defining a discrete model-independent measure of smoothness and comparing this measure for the Japanese and U.S. Treasury yield curves. We conclude that the underlying Japanese data includes spurious variation in forward rates due to the original yield curve smoothing methodology. We then limit the yield maturities used as inputs to the secondary smoothing process to those maturities consistent with “on the run” bond yields, yields of the most recently issued Japanese Government Bonds. We present videos comparing the original and revised data and present a comparison, also in video form, of the original Japanese forward rates and U.S. Treasury forward rates. We also compare the smoothness measures of Japanese and U.S. Treasury yield curves. We conclude that the revised Japanese data provides the best basis for fitting a multi-factor Heath, Jarrow and Morton model.
Section II outlines the process for determining whether the interest rate volatility for the factors driving the Japanese yield curve is constant (an “affine” model) or stochastic, typically expressed as a function of the level of interest rates. We note the extensive experience, relative to other markets, with negative interest rates in the Japanese Government Bond market. We conclude that the Japanese market, like other markets studied (with the possible exception of Thailand), is consistent with the stochastic volatility specification. Section III describes the process of fitting five different Heath, Jarrow and Morton models to Japanese Government bond yield data: models with 1, 2, 3, 6 and 10 factors. Section IV concludes the paper. The Appendix illustrates a sample model validation process for widely used one factor term structure models using Japanese and U.S. data.
I. Japanese Government Bond Data: Special Characteristics
A multi-factor term structure model is the foundation for best practice asset and liability management, market risk, economic capital, interest rate risk in the banking book, stress-testing and the internal capital adequacy assessment process. The objective in this paper is to illustrate the derivation of a multi-factor Heath Jarrow and Morton model of the Japanese Government Bond yield curve. As a by-product, the analysis reveals common data problems associated with yield curve histories and requires a standard methodology for quantification and resolution of those problems. Previous implementations of multi-factor Heath, Jarrow and Morton models have covered the following bond market sectors:
Australia Commonwealth Government Securities
Canada Government of Canada Securities
Germany German Bunds
Singapore Singapore Government Securities
Spain Spanish Government Bonds
Sweden Swedish Government Securities
Thailand Thai Government Securities
United Kingdom United Kingdom Government Bonds
United States U.S. Treasury Securities
We distinguish between our current findings and a prior paper on Japanese Government Bond term structure movements that covered the period from September 24, 1974 through December 30, 2015.
We explain differences in this paper’s conclusions from the prior paper below.
The first step in data model validation for the Japanese Government Bond market is to examine the historical availability of bond yields over time. This availability is summarized in Table I.
Table I
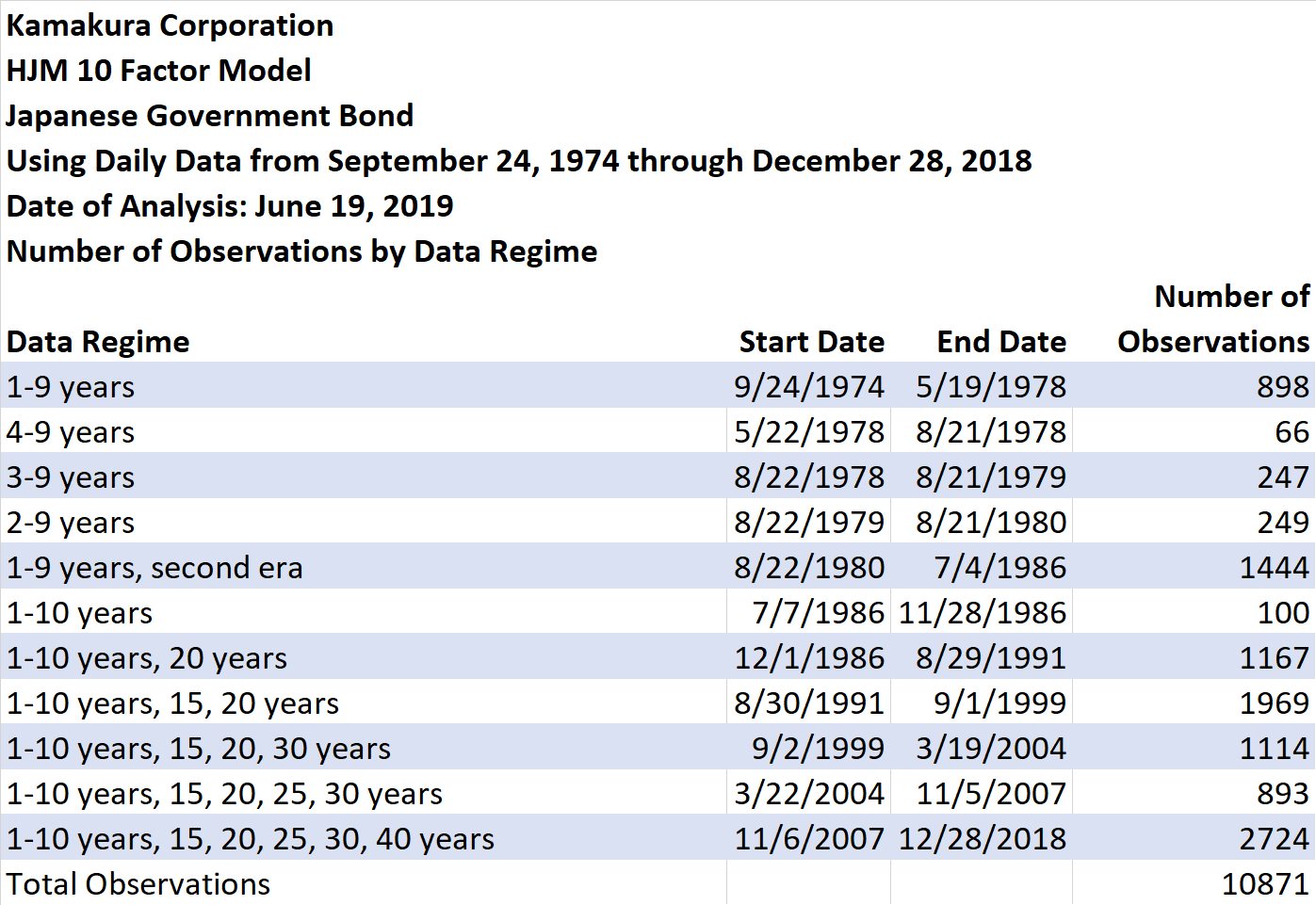
The data shows that the Ministry of Finance’s data history is typical in its occasional changes in “data regime,” i.e. which the maturities are available on a given date. By November 6, 2016, the Japan Ministry of Finance was providing 15 yields of 1 year or more, one of the highest degrees of granularity of the government bond markets studied so far. The yields provided by the Ministry of Finance were supplemented with Japanese government bill auction data reported separately by the Ministry of Finance.
Because the Heath, Jarrow and Morton analysis makes use of a yield curve with quarterly forward rate segments, the next step in data model validation is to fit quarterly forward rates to the raw coupon-bearing bond yields. The smoothness of the resulting forward rates will be a function of both the quality of the raw data from a smoothness point of view and the smoothness implied by the secondary smoothing process (that is, the method used in this paper to extract forward rates from the Ministry of Finance data). To ensure the maximum smoothness from the secondary smoothing process, we use the maximum smoothness forward rate methodology of Adams and van Deventer [1994], as corrected in van Deventer and Imai [1996]. Adams and van Deventer show that the maximum smoothness method overcomes the problems of the cubic spline approach of McCulloch, and, unlike the Svensson [1994] approach, allows for a perfect fit to the raw data provided by the Japan Ministry of Finance. See Jarrow [2014] for information on the problems with Svensson yield curve fitting.
We then conduct a visual inspection of the resulting forward rates implied by the raw data. The yield curve on June 4, 1986 in Exhibit I is representative:
Exhibit I

The forward rate curve is the smoothest curve that can be fit to the raw data provided by the Japan Ministry of Finance, but it implies much more forward rate variation than is typical for government yield curves. It also implies negative rates more than a decade before negative rates were observed in the Japanese government bond market. A video (analyzing data from an earlier paper) of the daily quarterly forward rates (in red) versus the zero coupon bond yields (blue) implied by the Ministry of Finance data on every business day through 2016 is given here:
https://www.youtube.com/watch?v=X49I1rIZPJg
If we count the daily local maxima and minima in the Japanese Government Bond forward rate curve implied by the data, we get many more “humps” than is typical in other markets. We can make this examination qualitatively by comparing the shape of the implied quarterly forward rates in the Japanese Government Bond market and the U.S. Treasury market on the same day from September 24, 1974 through December 30, 2016, as in this video:
https://www.youtube.com/watch?v=kP_BaNXC-58
Qualitatively, the Japanese Government forward rate curve is much more volatile than U.S. Treasury forward rates. The smoothness of the quarterly forward rate curve can be measured quantitatively using the quarterly forward rates implied by the Japanese Bond Market and U.S. Treasury yield curves. For a yield curve that consists of N quarterly forward rates, the discrete smoothness statistic at time t ZN(t) is the sum of the squared second differences in the forward rates, as explained by Adams and van Deventer [1994]. A continuous smoothing statistic can also be calculated when the functional form of the continuous forward rate is known.

A statistical comparison of smoothness for the unmodified Ministry of Finance data with data from the U.S. Department of the Treasury, both smoothed using the maximum smoothness forward rate approach, confirms that the first half of the Japanese Government Bond forward rate data set is much more volatile than the U.S. data, as the video shows.
We conclude that the raw data provided by the Japan Ministry of Finance implies unrealistic movements in forward rates. We seek to preserve the key insights of the data while removing the spurious volatility it implies. We do that by using only those long-term maturities at which the Japanese Government actually issues securities or for which there is a long and credible data history: 1 year, 2 years, 5 years, 9 (but not 10) years, 20 years, 30 years, and 40 years. We add the 3 month and 6-month bill rates using auction results when available. These abridged maturities were used for a modified smoothing process
The final “on the run” quarterly forward rates and zero coupon bond yields used to fit the Heath, Jarrow and Morton models are given in this video on a daily basis from September 24, 1974 to December 30, 2016:
https://www.youtube.com/watch?v=hdGTMDApgt4
II. Constant versus Stochastic Volatility
Constant volatility (“affine”) term structure models are commonly used for their ease of simulation and estimation of “future expected rates” in order to determine the “term premium” in current yields. Prominent examples are Adrian, Crump and Moench [2013], Kim and Wright [2005], and Duffie and Kan [1996]. On the other hand, the weight of the empirical evidence in most of the countries studied to date indicates that interest rate volatility does vary by the level of the corresponding forward rate. To illustrate that fact, we studied the shortest forward rate on the U.S. Treasury curve on a daily basis from January 2, 1962 through December 28, 2018. We ordered the data from lowest forward rate level to highest forward rate level. We formed non-overlapping groups of 25 observations each and calculated both the standard deviation of 91-day forward rate changes and the mean beginning-of-period forward rate in each group. The results are plotted in Exhibit III:
Exhibit III
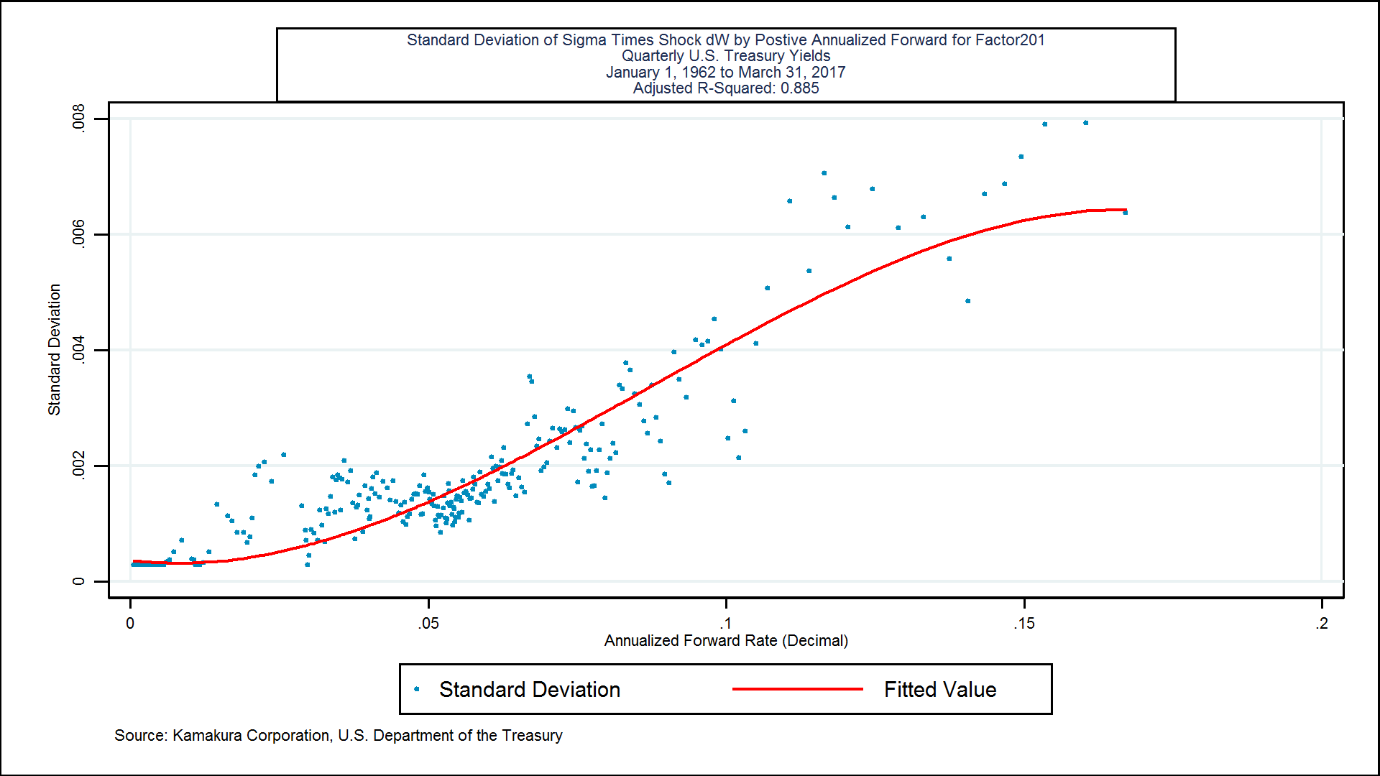
A cubic function of annualized forward rates explains 88.5% of the variation in the standard deviation of forward rate changes for these ordered groups. Note that the right-hand side of the curve has been constrained to have a first derivative of zero at a high level of rates. This phenomenon has been confirmed in the government securities markets for Australia, Canada, Germany, Japan, Singapore, Spain, Sweden, Thailand, the United Kingdom, and the United States. Exhibit IV shows the results for the first risk factor in the Japanese Government Bond market, the first forward rate:
Exhibit IV

Using the on the run maturities for Japanese Government Bond yields, the cubic stochastic volatility specification explains 73.2% of the observed variation in forward rate volatility in the first forward rate on the Japanese Government Bond yield curve. We have imposed the same constraint on the first derivative and require that the fitted volatility not be less than the observed volatility when interest rates are negative, which we discuss later in this section.
Exhibit V shows the historical movements in Japanese Government Bond zero coupon yields over the historical period studied:
Exhibit V

Exhibit VI below shows the evolution of the first quarterly forward rate (the forward that applies from the 91st day through the 182nd day) over the same time period:
Exhibit VI

We use three statistical tests to determine whether or not the hypothesis of normality for forward rates and zero coupon bond yields should be rejected at the 5% level: the Shapiro-Wilk test, the Shapiro-Francia test, and the skew test, all of which are available in common statistical packages. The results of these tests are summarized in Table II:
Table II
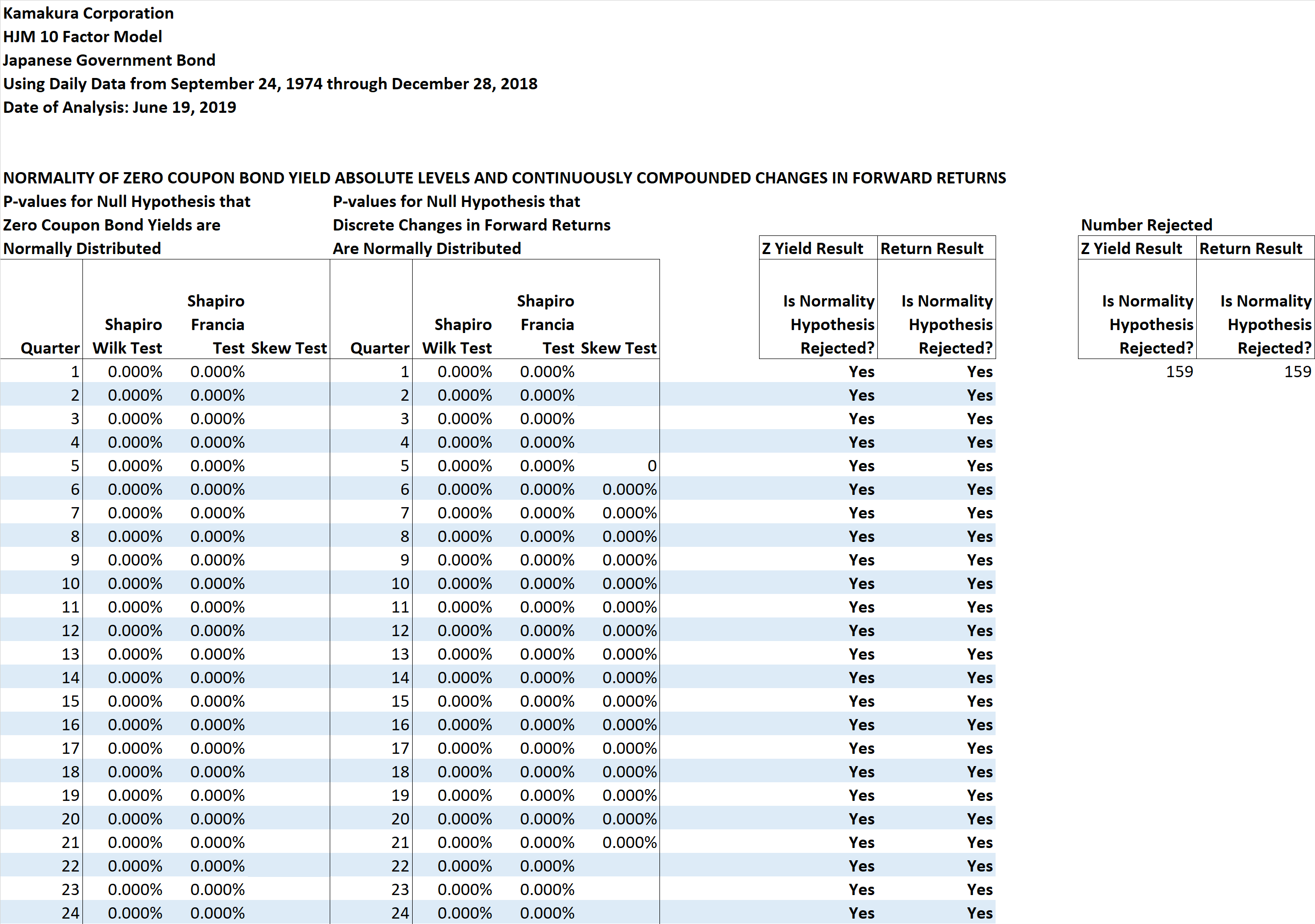
Table II above shows the p-values for these three statistical tests for the first 24 quarterly maturities. We conduct the test for each quarter out to 40 years, the longest maturity used in the smoothing process. The null hypothesis of normality is rejected by all 3 tests for 159 of the 159 quarterly zero coupon yield maturities. For quarterly changes in forward rates, the null hypothesis of normality is again rejected by all 3 tests for all 159 of the 159 maturities for changes in forward rates. This is a powerful rejection of the normality assumptions implicit in constant coefficient or “affine” term structure models. In most of the other countries studied, the hypothesis of normality has been rejected strongly as well. Given these results, we proceed with caution on the implementation of the affine model.
In Chapter 3 of Advanced Financial Management (second edition, 2013), van Deventer, Imai and Mesler analyze the frequency with which U.S. Treasury forward rates move up together, down together or remain unchanged. This exercise informs the Heath, Jarrow and Morton parameter fitting process and is helpful for the model validation questions posed in the Appendix. We perform the yield curve shift analysis using 10,898 days of zero coupon bond yields for the Japanese Government Bond yield curve. We analyze the daily shifts in the zero coupon bond yields on each business day from September 24, 1974 through December 28, 2018. The results are given in Table III:
Table III

Yield curve shifts were all positive, all negative, or all zero 10.36%, 1.04%, and 0.00% of the time, a total of 11.40% of all business days. The predominant yield curve shift was a twist, with a mix of positive changes, negative changes, or zero changes. These figures are similar to those for the U.S. Treasury, German Bund, Government of Canada, and United Kingdom Government Bond yield curves. These twists, which happen 88.60% of the time in Japan, cannot be modeled accurately with the conventional implementation of one factor term structure models.
Another important aspect of yield curves is the number of local minima and maxima that have occurred over the modeling period. The results for the Japanese Government Bond Market are given in Table IV:
Table IV

The number of days with 0 or 1 humps (defined as the sum of local minima and maxima on that day’s yield curve) was 76.12% of the total observations in the data set.
Finally, before proceeding, we count the number of occurrences of negative rates for each forward rate segment of the yield curve over the history provided by the Japan Ministry of Finance and report on the observed 91-day volatility of forward rates when the start of the period annualized forward rate is negative, zero, and positive.
Table V

The table shows that the volatility of forward rate changes could be calculated for the first forward rate on 789 observation dates when that forward rate was negative. The 91-day volatility was 0.000185 (that is 0.0185%). For the 9917 observation dates for which the first forward rate was positive, the volatility over 91 days was 0.001319 (i.e. 0.1319%). For other forward rate maturities, the volatility of the negative rate observations gradually increased with maturity. We emphasize two obvious points: rates can be and have been negative, and, when rates hit zero and below, interest rate volatility is not zero. It is positive but at a much lower level than for positive forward rate observations.
III. Fitting Heath, Jarrow and Morton Parameters
A simple first step in constructing a multi-factor Heath, Jarrow and Morton model is to conduct principal components analysis on the forward rates that make up the relevant yield curve. For the Japanese Government Bond market, at its longest maturity, these quarterly segments consist of one three-month spot rate and 159 forward rates. For purposes of exposition, we concentrate on larger data set with a maximum maturity of 30 years, or 119 forward rates. Over 4631 observations, the principal components analysis indicates in Table VI that the first factor explains only 68.93% of the movement in forward rates over the full curve. For a high degree of explanatory power, the principal components analysis indicates that 8 to 9 factors will be necessary.
Table VI

With this analysis as background, we begin the Heath, Jarrow and Morton fitting process.
In the studies done so far, the number of statistically significant factors are summarized below:
Australia: Commonwealth Government Securities, 14 factors
Canada: Government of Canada Securities, 12 factors
Germany: Bunds, 14 factors
Japan: Japanese Government Bonds, 8 factors
Singapore: Singapore Government Securities, 9 factors
Spain Spanish Government Securities, 11 factors
Sweden: Swedish Government Securities, 11 factors
Thailand Thai Government Securities, 11 factors
United Kingdom: Government Securities, 14 factors
United States: Treasury Securities, prior version 10 factors
Note that our prior term structure model fitting exercise for the Japanese Government Bond market resulted in 8 to 16 statistically significant factors.
We now fit a multi-factor Heath, Jarrow and Morton model to Japanese Government Bond zero coupon yield data from September 24, 1974 to December 28, 2018. For computational simplicity, we use the compress the 11 data regimes numbered in the right hand column of Table I to four regimes. The first is for observations where no maturity longer than 9 years was reported. The second is for those observations where no maturity longer than 20 years was reported. The third regime and fourth regimes add observations with maturities from 20 to 30 years and 30 to 40 years respectively.
The procedures used to derive the parameters of a Heath, Jarrow and Morton model are described in detail in Jarrow and van Deventer (June 16, 2015 and May 5, 2017).
We followed these steps to estimate the parameters of the model:
- We extract the zero coupon yields and zero coupon bond prices for all quarterly maturities out to 30 years for all daily observations for which the 30 year zero coupon yield is available. For other observations, we extended the analysis to the longest maturity available, which varies by data regime. This is done using Kamakura Risk Manager, version 10.0, using the maximum smoothness forward rate approach to fill the quarterly maturity gaps in the zero coupon bond data.
- We use overlapping 91-day intervals to measure changes in forward rates, avoiding the use of “quarterly” data because of the unequal lengths of calendar quarters. Because overlapping observations trigger auto-correlation, “HAC” (heteroscedasticity and autocorrelation consistent) standard errors are used. The methodology is that of Newey-West with 91 day lags.
- We consider ten potential explanatory factors: the idiosyncratic portion of the movements in quarterly forward rates that mature in 6 months, 1 year, 1.5, 2, 3, 5, 7, 10, 20, and 30 years. Ten factors are required by the Bank for International Settlements market risk guidelines published in January 2016 and relevant to the Fundamental Review of the Trading Book.
- We calculate the discrete changes in forward returns as described in the parameter technical guide. Because the discrete changes are non-linear in the no-arbitrage framework of Heath, Jarrow and Morton, we use non-linear least squares to fit interest rate volatility.
- We use a different non-linear regression for each segment of the yield curve. We considered a panel-based approach, but we rejected it for two reasons: first, the movement of parameters as maturity lengthens is complex and not easily predictable before estimation; second, the residual unexplained error in forward rates is very, very small, so the incremental merit of the panel approach is minimal.
- We then begin the process of creating the orthogonalized risk factors that drive interest rates using the Gram-Schmidt procedure. These factors are assumed to be uncorrelated independent random variables that have a normal distribution with mean zero and standard deviation of 1.
- Because interest volatility is assumed to be stochastic, simulated out-of-sample forward rates will not in general be normally distributed. We also calculate constant volatility parameters and choose the most accurate from the constant volatility and stochastic volatility models estimated.
- In the estimation process, we added factors to the model as long as each new factor provided incremental explanatory power. The standard suite of models in both cases includes 1 factor, 2 factors, 3 factors, 6 factors and “all factors,” which varies by country.
We postulate that interest rate volatility for each forward rate maturity k is a cubic function of the annualized forward rate that prevails for the relevant risk factor j at the beginning of each 91-day period:

Because of the volatility data reported above, we expect b0,jk to be close to 0.018553%.
We use the resulting parameters and accuracy tests to address the hypothesis that a one factor model is “good enough” for modeling Japanese Government Bond yields in the Appendix. We report the accuracy results for 1, 2, 3, 6 and 10 factors. The factors are the idiosyncratic variation in quarterly forward rates at each of 10 maturities. The factors, described by the maturity of the forward rate used, are added to the model in this order:
Factor 1: 6 months
Factor 2: 9 years
Factor 3: 3 years
Factor 4: 7 years
Factor 5: 1 year
Factor 6: 5 years
Factor 7: 2 years
Factor 7: 20 years
Factor 9: 30 years
Factor 10: 40 years
Exhibit VII summarizes the adjusted r-squared for the non-linear equations for each of the 159 quarterly forward rate segments that make up the Japanese Government Bond yield curve:
Exhibit VII

The adjusted r-squared for the best practice model over each of the forward rates is plotted in blue and is near 100% for all 159 quarterly segments of the yield curve. The one factor model in red, by contrast, does a poor job of fitting 91-day movements in the quarterly forward rates. The adjusted r-squared is good, of course, for the first forward rate since the short rate is the standard risk factor in a one factor term structure model. Beyond the first quarter, however, explanatory power declines rapidly. The adjusted r-squared of the one factor model never exceeds 30% after the first 25 quarterly forward rates and is below that level at most maturities.
IMPORTANT NOTE: The 16 factors found to be statistically significant in a prior version of the model, through June 30, 2015, used Ministry of Finance data “as is” as inputs to the smoothing process. Having subjected this data to the intense due diligence described earlier in this note, we conclude that 6 of the initial 16 factors were spurious factors caused by a Ministry of Finance smoothing process that ignored the “scientific knowledge” known to experienced yield curve modelers: yield curves should be smooth, and, when they are not, there is most likely a series of data errors.
The root mean squared error for the 1, 2, 3, 6 and 10 factor constant coefficient model is shown in Exhibit VIII.
Exhibit VIII

The root mean squared error for the 10-factor model is less than 0.0015% at every maturity along the yield curve. This result should not come as a surprise to a serious analyst, because it is very similar to the results of the best practice Heath, Jarrow and Morton term structure models for U.S. Treasuries, Government of Canada Bonds, French Government Bonds, Italian Government Bonds, United Kingdom Government Bonds, German Bunds, Australian Commonwealth Government Securities, Russian Government Securities, Singapore Government Securities, Spanish Government Securities, Swedish Government Securities, and Thai Government Bond yields.
Bayesian Considerations in Model Validation
Kamakura term structure model validation is conducted in the spirit of Bayesian iterative model building as outlined by Gelman et al. A detailed paper on these methodologies in the context of the U.S. Treasury Heath Jarrow and Morton model is forthcoming in the near future.
IV. Conclusion
The Japanese Government Bond yield curve is driven by 10 factors, a number of factors very similar to government yield curves in 12 other markets for which studies have been conducted. The 1974-2018 yield history for Japan is relatively long and it spans a wide range of interest rate experience.
The task of estimating interest rate volatility was slightly complicated by the yield curve smoothing methods employed by the Ministry of Finance through the year 2000. Standard model validation procedures revealed that this yield data implied implausible variation in forward rates, which would distort measured interest rate volatility. To avoid this, we restricted the long term yields used as input to the maximum smoothness forward rate process to maturities close to the maturities at which the Japanese Government is a regular bond issuer. Given this modified data set, the stochastic volatility assumption provided more accurate and more reasonable parameters than a constant volatility model, particularly in the context of Bayesian simulations as part of the model validation process. Exhibit IX summarizes the reasons for those conclusions:
Exhibit IX

The vertical axis lists the maturities used as risk factors by years to maturity of the underlying quarterly forward rate. The risk factors are the idiosyncratic movement of each of these forward rates. If the risk factor is statistically significant in explaining the movement of forward rates with the quarterly maturities listed on the horizontal axis, a dot is placed in the grid. Note that the quarterly forward rate maturing in 40 years is only used as an explanatory variable for maturities of 30 years and longer. Similarly, the quarterly forward rates maturing in 20 and 30 years are only used as explanatory variables for maturities of 9 years and longer and 20 years and longer, respectively.
The nature of interest rate volatility for each combination of risk factor maturity and forward rate maturity is color coded. If the derived volatility is constant, the color code is orange. This is the affine specification. The graph shows immediately that a small minority of the risk factor maturity/forward rate maturity volatilities are consistent with the affine structure. The green and blue codes address the issue of whether interest rate volatility for that combination of risk factor maturity and forward rate maturity is zero when the forward rate level is zero. If the measured volatility at a zero forward rate level is zero, the color code is green. Otherwise the color code is blue.
The chart summarizes the fact that all 10 factors are statistically significant across the yield curve for Japanese Government Bonds. The dominant derived interest rate volatility is the cubic stochastic volatility specification with a non-zero constant. An affine assumption for interest rate volatility is best fitting for a minority of the combinations of risk factor maturity and forward rate maturity.
Appendix: Model Validation Issues for 1-Factor Models
In spite of the overwhelming evidence across countries that government bond yields are driven by multiple factors, the use of single factor term structure models in interest rate risk management systems remains common even in some of the world’s largest banks. This appendix asks and answers a number of important questions on the use of one factor models that any sophisticated model audit would pose. Given the answers below, most analysts would conclude that one factor term structure models are less accurate than a long list of multi-factor term structure models and that the one factor models would therefore fail a model audit.
We address two classes of one factor term structure models, all of which are special cases of the Heath, Jarrow and Morton framework, in this appendix using data from the U.S. Treasury market. Answers for other government bond markets cited in the references are nearly identical.
One factor models with rate-dependent interest rate volatility;
Cox, Ingersoll and Ross (1985)
Black, Derman and Toy (1990)
Black and Karasinski (1991)
One factor models with constant interest rate volatility (affine models)
Vasicek (1977)
Ho and Lee (1986)
Extended Vasicek or Hull and White Model (1990, 1993)
Non-parametric test 1: Can interest rates be negative in the model?
The one factor models with rate-dependent interest rate volatility make it impossible for interest rates to be negative. Is this implication true or false? It is false, as Deutsche Bundesbank yield histories, Swedish Government Bond histories, U.S. Treasury histories, Japanese Government Bond yields and yields in many other countries show frequent negative yields in in recent years. Table V and this video of forward rates and zero coupon bond yields for the Japanese Government Bond yield curve documents the existence of negative forward rates using daily data from September 24, 1974 through December 30, 2016:
www.youtube.com/watch?v=X49I1rIZPJg
Non-parametric test 2: As commonly implemented, one factor term structure models imply that all yields will either (a) rise, (b) fall, or (c) remain unchanged. This implication is false, as documented for Japan in Table III. In fact, yield curves have twisted on 88.60% of the observations for the Japanese Government Bond market.
Non-parametric test 3: The constant coefficient one-factor models imply that zero coupon yields are normally distributed and that changes in zero coupon yields are also normally distributed. In the Japanese Government Bond market, this implication is rejected by three common statistical tests for 159 of 159 quarterly maturities for zero yields and for all 159 of the quarterly changes, as shown in Table II.
Assertion A: There are no factors other than the short term rate of interest that are statistically significant in explaining yield curve movements.This assertion is false. Table VI shows, using principal components analysis, that 8-10 factors are needed to explain the movements of the Japanese Government Bond yield curve. Exhibit IX makes the same point in more detail.
Assertion B: There may be more than one factor, but the incremental explanatory power of the 2nd and other factors is so miniscule as to be useless. This assertion is false, as the 2nd through 10th factors in the Japanese Government Bond market explain 31.07% of forward rate movements, compared to 68.93% for the first factor alone. In most countries, the best “first factor” is not the short rate of interest used by many large banks; it is the parallel shift factor of the Ho and Lee model.
Assertion C: A one-factor “regime shift” model is all that is necessary to match the explanatory power of the 2nd and other factors.This assertion is also false. A recent study prepared for a major U.S. bank regulator also confirmed that a one factor “regime shift” term structure model made essentially no incremental contribution toward resolving the persistent lack of accuracy in one factor term structure models.
REFERENCES
Adams, Kenneth J. and Donald R. van Deventer, “Fitting Yield Curves and Forward Rate Curves with Maximum Smoothness,” Journal of Fixed Income, 1994, pp. 52-61.
Adrian, Tobias, Richard K. Crump and Emanuel Moench, “Pricing the Term Structure with Linear Regressions,” Federal Reserve Bank of New York, Staff Report 340, August 2008, revised August 2013.
Angrist, Joshua D. and Jorn-Steffen Pischke, Mostly Harmless Econometrics: An Empiricist’s Companion, Princeton University Press, Princeton, 2009.
Berger, James O. Statistical Decision Theory and Bayesian Analysis, second edition, Springer-Verlag, 1985.
Berry, Donald A. Statistics: A Bayesian Perspective, Wadsworth Publishing Company, 1996.
Campbell, John Y, Andrew W. Lo, and A. Craig McKinley, The Econometrics of Financial Markets, Princeton University Press, 1997.
Gelman, Andrew and John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin, Bayesian Data Analysis, third edition, CRC Press, 2013.
Goldberger, Arthur S. A Course in Econometrics, Harvard University Press, 1991.
Hamilton, James D. Times Series Analysis, Princeton University Press, 1994.
Hansen, Bruce E. Econometrics, University of Wisconsin, January 15, 2015.
Hastie, Trevor, Robert Tibshirani and Jerome Friedman, Elements of Statistical Learning: Data Mining, Inference and Prediction, Springer, second edition, tenth printing, 2013.
Heath, David, Robert A. Jarrow and Andrew Morton, “Bond Pricing and the Term Structure of Interest Rates: A Discrete Time Approach,” Journal of Financial and Quantitative Analysis, 1990, pp. 419-440.
Heath, David, Robert A. Jarrow and Andrew Morton, “Contingent Claims Valuation with a Random Evolution of Interest Rates,” The Review of Futures Markets, 9 (1), 1990, pp. 54 -76.
Heath, David, Robert A. Jarrow and Andrew Morton,” Bond Pricing and the Term Structure of Interest Rates: A New Methodology for Contingent Claim Valuation,” Econometrica, 60(1),1992, pp. 77-105.
Heath, David, Robert A. Jarrow and Andrew Morton, “Easier Done than Said”, RISK Magazine, October, 1992.
Jarrow, Robert A. Modeling Fixed Income Securities and Interest Rate Options, second edition, Stanford University Press, Stanford, 2002.
Jarrow, Robert A. and Stuart Turnbull, Derivative Securities, second edition, South-Western College Publishing, Cincinnati, 2000.
Jarrow, Robert A. and Donald R. van Deventer, “Monte Carlo Simulation in a Multi-Factor Heath, Jarrow and Morton Term Structure Model,” Kamakura Corporation Technical Guide, Version 4.0, June 16, 2015
Jarrow, Robert A. and Donald R. van Deventer, “Parameter Estimation for Heath, Jarrow and Morton Term Structure Models,” Kamakura Corporation Technical Guide, Version 4.0, May 5, 2017.
Johnston, J. Econometric Methods, McGraw-Hill, 1972
Kim, Don H. and Jonathan H. Wright, “An Arbitrage-Free Three Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates,” Finance and Economics Discussion Series, Federal Reserve Board, 2005-33.
Maddala, G. S. Introduction to Econometrics, third edition, John Wiley & Sons, 2005.
Papke, Leslie E. and Jeffrey M. Wooldridge, “Econometric Methods for Fractional Response Variables with an Application to 401(K) Plan Participation Rates,” Journal of Applied Econometrics, Volume 11, 619-632, 1996.
Robert, Christian P. The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, second edition, Springer Science+Business Media LLC, 2007.
Stock, James H. and Mark W. Watson, Introduction to Econometrics, third edition, Pearson/Addison Wesley, 2015.
Studenmund, A. H. Using Econometrics: A Practical Guide, Addison-Wesley Educational Publishers, 1997.
Theil, Henri. Principles of Econometrics, John Wiley & Sons, 1971.
van Deventer, Donald R. “Essential Model Validation for Interest Rate Risk and Asset and Liability Management,” an HJM model for the U.S. Treasury curve, Kamakura Corporation working paper, www.kamakuraco.com, February 11, 2015.
van Deventer, Donald R. “Model Validation for Asset and Liability Management: A Worked Example” using Canadian Government Securities, Kamakura Corporation working paper, www.kamakuraco.com, July 20, 2016.
van Deventer, Donald R. “Interest Rate Risk: Lessons from 2 Decades of Low Interest Rates in Japan,” Kamakura Corporation working paper, www.kamakuraco.com, August 11, 2016.
van Deventer, Donald R. “A Multi-Factor Heath Jarrow and Morton Model of the United Kingdom Government Bond Yield Curve,” Kamakura Corporation working paper, www.kamakuraco.com, August 17, 2015.
van Deventer, Donald R. “A Multi-Factor Heath Jarrow and Morton Model of the German Bund Yield Curve,” Kamakura Corporation working paper, www.kamakuraco.com, August 21, 2015.
van Deventer, Donald R. “A Multi-Factor Heath Jarrow and Morton Model of the Australia Commonwealth Government Securities Yield Curve,” Kamakura Corporation working paper, www.kamakuraco.com, August 27, 2015.
van Deventer, Donald R. “A Multi-Factor Heath Jarrow and Morton Model of the Swedish Government Bond Yield Curve,” Kamakura Corporation working paper, www.kamakuraco.com, September 3, 2015.
van Deventer, Donald R. “Spanish Government Bond Yields: A Multi-Factor Heath Jarrow and Morton Model,” Kamakura Corporation working paper, www.kamakuraco.com, September 10, 2015.
van Deventer, Donald R. “Singapore Government Securities Yields: A Multi-Factor Heath Jarrow and Morton Model,” Kamakura Corporation working paper, www.kamakuraco.com, September 22, 2015.
van Deventer, Donald R. “The Regime Change Term Structure Model: A Simple Model Validation Approach,” Kamakura Corporation working paper, www.kamakuraco.com, January 26, 2016.
van Deventer, Donald R., Kenji Imai and Mark Mesler, Advanced Financial Risk Management, second edition, John Wiley & Sons, Singapore, 2013.
Woolridge, Jeffrey M. Econometric Analysis of Cross Section and Panel Data, The MIT Press, 2002.



